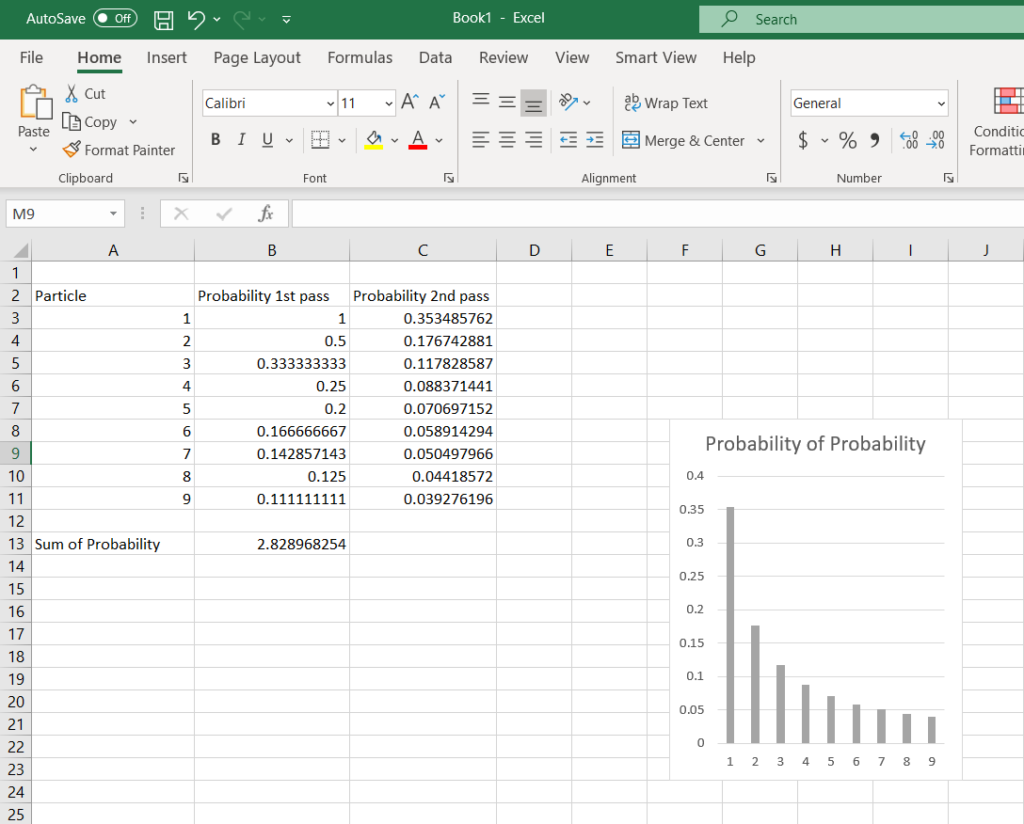
To find the probabilities of probabilities.
最近偶然读到一些谈论本福特定律的文章。发现作者们都声称本福特定律没有严格的数学证明。这种说法让我很费解。
也许是因为本科学习地球与空间科学的原因,再加上现在天天接触多维数据库,本福特定律的严格的数学证明在我看来再明显不过了。
宇宙中如果按原子核颗粒数的话,原子序数为1和2的元素(氢和氦)几乎占100%,因为原子序数大的元素的颗粒,是多个原子序数小的颗粒加起来的和。所以原子序数大的元素颗粒总数,出现的概率总会比原子序数小的元素出现的概率小。这种原子序数,和颗粒总数出现的概率的反比例关系,在自然数中也存在。因为自然数的出现,就是古人用来表示颗粒的数学符号。自然界中:
. (出现概率为 1)
.. (出现概率为 1/2)
… (出现概率为 1/3)
…. (出现概率为 1/4)
如此类推下去到,
……… (出现概率为 1/9)
将1到9数学符号所代表的本质的颗粒数,出现的概率做为一个新的单位(新的一维)。对概率求概率。画出来的曲线如下。这样的曲线适合于自然界中许多通过积累才能从小变大,进阶晋级的数。例如:1,积累足够才能到9;10,积累足够才能到90;100,积累足够才能到900……
门牌号编号,小的号码编够了才能有大的门牌号……
还有标价,小的价格标够了才会标到昂贵的价格……
数学是上帝的语言、神的语言、上天的语言。以上,我们用数学描写了自然科学和社会科学中的以下公式和格言:
- 群众是真正的英雄+英雄是群众中的少数
- 小人是真正的君子+君子是小人中的极品
- 民贵君轻+君为民主